
(1908-1994)
大师简介
1908年,Max Bill出生于瑞士东北部温特苏的一个钟表世家
从年轻时候开始,Max Bill就显示出超人一等的设计天赋,1927年,19岁的Max Bill慕名前往德国包豪斯设计学院就读,学习当时颇为新潮的包豪斯设计理念。 在包豪斯设计学院,Max Bill遇到了他生命中的恩师——学院第一任校长Walter Gropius
在当时靡靡之风盛行的欧洲,格罗皮乌斯讲究功能、技术和经济效益统一的设计理念让Max Bill大为震动,也让Max Bill开始用理性的、科学的思维来重新考量设计艺术
“向死的机械产品注入灵魂”,Walter Gropius的这句话也成为Max Bill日后的设计精髓。 随后的30年间,欧洲乃至世界都经历了巨大的震荡,政治、战争、民族解放……时代已在剧变
1956年,Max Bill在带领他在乌尔姆设计学院的学生开发一款厨房用钟
1957年Max Bill离开乌尔姆设计学院学校,重新创建自己的工作室,主要从事雕塑及绘画工作
1993,他获得由日本天皇授予的高松宫殿下纪念世界文化奖之雕塑奖
1994年,Max Bill先生在柏林去世
马克思·比尔—20年代末新平面设计的核心人物,瑞士构成主义派的领导者,瑞士著名的包豪斯学者、建筑师,产品设计师,艺术家,画家,字体设计师,工业设计师和平面设计师 。

(工作中的马克思·比尔)
设计风格
马克思·比尔充分的应用数学与艺术相结合的创作手法。并极至地展现出具体艺术点、线、面的艺术特点。在他的作品中,我们能够非常直观地看到艺术家整个创作过程的思维轨迹。
作品赏析


(马克思·比尔—乌尔姆教学楼)

(马克思·比尔—我)

(《设计为主题的3 – 4 – 5》,1980,风格:具体主义,类型:抽象)
同一主题下的十五变异系列(Fifteen Variations on a Single Theme)①是比尔在1938年(30岁)创作的一套代表性的作品。从中我们能够较为清晰地理解数理模式是如何作为一种”指导性”的原则整合到他的艺术作品之中的。
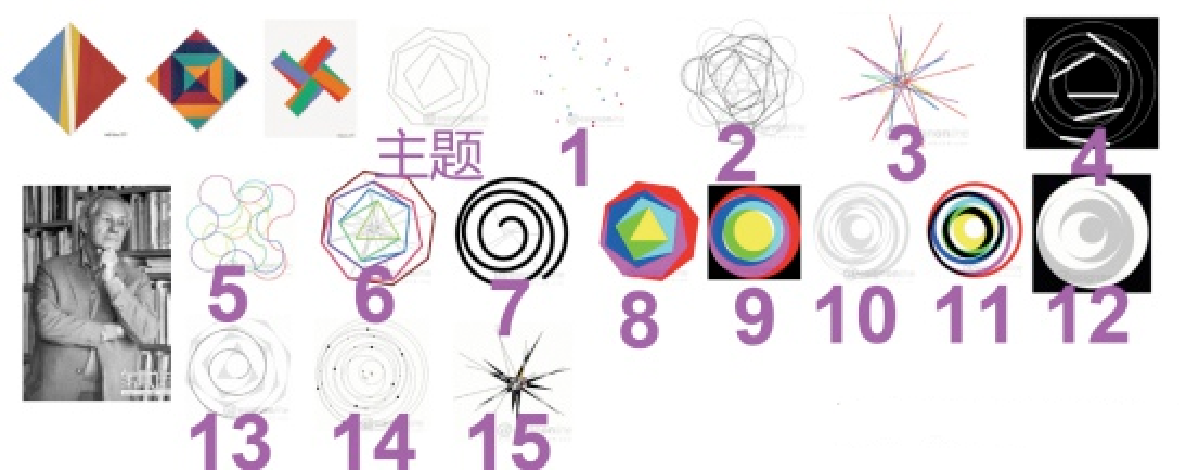
主题:中心由一个不断向外延展的等边三角形构成,等边三角形的第三边被向外展开,并继续以同样长度的线段向外延伸,与等边三角形的第二边构成平行线段,进而形成一个继续向外延展的正方形,并以同样的方式进一步形成正五边形、六边形……并最终形成一个可以继续延展的等八边形。从中,我们可以看出,最初的等边三角形中的一条边被单独打开,作为第一个正多边形的结束,并成为下一个正多边图形的开始。同时,这条边被作为一条单元线条被不断复制延展,每一次展开的角度都决定了下一个正多边形的边数。这样,一条条同样长度的线段首尾相接在一起,不断地向外延展,即说明了变化中的规律性,又有着一种无限扩张的张力被表现出来,形成了看似完成又可无限延展的规律性图形。
图1:变异将主题图形中各个正多边形的顶点以小色点表现出来,并略去主题图形中的线,单一颜色色点为正多边形中的独立部分,混合色点表现当前正多边形与下一个正多边形共用部分,色点颜色的选取及变化规律并以此无限延展。
图2:变异基本骨架由主题图形构成,将主题图形中的单元边作为每一个添加圆形的直径,并依次无限延展,形成一个由圆形构成的无限展开体。同时,将每个正多边形的展开部分以等长度的半圆闭合,作为由等边三角形到正八边形的间隔部分。图形骨架虽由主题而来,但最终表现为以正多边形展开边为直径的圆形构成,并可无限延展的圆形和半圆的组合。
图3:主题由线到点构成变异,进一步由点到线构成变异,主题图形为多边形的各个顶点以线首尾相连,与主题不同的是,将主题的各个顶点延伸为线段分别指向正多边形的中心,形成了由内至外无限延展的放射性线条组合。
图4:变异同样省略掉主题部分首尾相连的线,以多个由小至大组合的圆形构成了新的图形,第一个圆形以等边三角形的三个顶点为共圆点,第二个圆形以正方形的四个顶点为共圆点,并以此类推到最外围的圆形。同时,在变异中,主题图形中的展开部分被较粗的等长线段”闭合”,最终形成了由圆形和等长线段构成的螺旋状的富有节奏的图形。
图5:变异进一步将主题中的各个顶点以半圆首尾相连构成,每一个相接的半圆都与前一半圆的方向相反,半圆的颜色与变异相一致。进而构成了可无限延展的彩色线条。
图6:在变异的基础上进行边缘着色,将变异中的彩色面略去,保留边缘线,所以形成两条相并列的彩色线段闭合而成的正多边图形的组合。由外到内形成了从深到浅的色彩渐变,进而产生一种线性旋涡并不断放射扩张的视觉冲击效果。
图7:变异由六段不同的圆弧组成运动的螺旋形,这种螺旋形的运动轨迹取决于主题几何图形对角线的长短。圆弧与圆弧之间的交点为相邻两个几何形与圆的共切点。
图8:在变异中,所有的展开的正多边形都被闭合起来。同时,每一个正多边形都被赋予了相应的色彩,这使得每个正多边形的区域被清楚地划分出来。形成了黄~绿~青~蓝~紫~红的循环过程,既体现出图形的延展规律又表达出色彩变化规律。与主题相同的是,变异也是可以无限延展的。
图9:变异由六个与主题几何图形相切的圆组成,圆形色彩的搭配按照相对应的几何图形的色彩。相邻两个圆之间叠加的部分显示为白色。形成由内到外旋转的色带效果。
图10:变异由主题图形的每一个正多边形为依据画出内切圆和外切圆组成的粗状圆环,六个圆环彼此重叠的区域显示为白色,反之用灰色表示。最终画面产生强烈的旋转和向外无限扩张的视觉冲击感。
图11:变异以主题图形的每一个正多边形为依据画出内切圆和外切圆而构成的粗状彩色圆环,这些圆环相互穿插和重叠,重叠部分显示为黑色,最终表现为多个色环交错缠绕的视觉效果。
图12:变异是在主题图形的每一个正多边形为依据画一个内切圆,呈现出不同半径的圆相互重叠的图形,重叠部分和非重叠部分分别用白和灰进行表示,就形成了圆与实心半圆弧的图底关系。
图13:变异以主题图形为骨架,将主题图形中的各个正多边形分别添入内切圆,并将首尾相连具有同一切点的半圆连在一起,形成了一条圆的渐开线。同时,圆形与多边形相减的部分被添入了灰色,灰色部分同样形成一条向外无限展开的螺旋状图形,此图形与之前的圆形渐开线以不同方向、不同节奏逆向螺旋向外无限展开。并且,由于两个图形的展开方向不同反而达到了互相增强的效果。
图14:变异以主题中的各个封闭的正多边形为依据绘制出内切圆和外接圆,在外接圆与外接圆的相交处以大的黑点加以标注,其他形式的交点均用小的黑点加以标注。同时,画面中心的六个彩色小点,由黄至红分别代表正三角形到正八边行的中心位置。
图15:在外围的闭合区域和重叠区域分别用黑和白表示,而中心由多边形对角线所构成闭合区域的颜色分别用其所对应的几何形的色彩,形成放射性的绚目效果。
在以上作品的分析过程中,我们不难发现这一系列艺术作品形成过程所贯穿的艺术思想。在这一系列作品中,艺术家首先制定出一个数学规则,并将这一数学规则以图表的曲线形式表现在”主题”当中。在这里与其说”主题”是一条可以无限延展的渐开线段组合,不如说他是某一数学函数的图解。他十分清晰直观地表达出了艺术家创作这一系列作品所应用的基础的数学规则,并在这一规则基础之上,不断地将新的数学规律添加到各个变异之中去。各种新的数学规则最终以图形、色彩的形式表现出来。然而仅凭审美直觉是无法理解这一系列的图形、色彩的内在规律的,这就要求读者站在一个全新的视角,用”解析几何的方式”去欣赏比尔的艺术作品,以理性的分析贯穿于审美直觉的始终。就像艺术家本人所说的那样,作品来自纯粹的精神世界,而解读作品所需要的是对视觉符号的一种纯粹的感知和理解的过程,也就是说这是一种视觉和心理相统一的过程。在这一过程中,我们不仅看到了整个系列作品形成的过程,同时,又仿佛被带入了艺术家所构建的纯粹的精神世界之中,这是一种超脱于自然之外的心理自然,一种数学和艺术携手共建的自然。在这一自然中,数学成为了艺术创作手段,表现出各种绚丽的色彩、线条,而艺术则讲述着数学语言,并在各个环节贯穿着数字信息。

(太阳灯,1951,风格:建构主义,类型:雕塑)

1954年比尔设计的Ulmer Hocker凳强烈地体现了比尔追求功能及主张运用纯粹的几何造型的理念。同时既能够当做小凳子,也可以当做是席地而坐的小桌。

1957年比尔设计的壁钟,因为这件产品更加充分地说明了比尔是多么地强调功能在设计中的重要性,设计的精华就在于其简洁的外表、纯粹的线条及优秀的可识别性。这件作品被誉为新功能主义的典范。

(Four Identical Large Parts III,1959,风格:具体主义,类型:抽象)

从1961年开起,Max Bill开始设计包豪斯风格腕表,在JUNGHANS的打造下,经典设计与顶尖技术完美融合,包豪斯款式腕表开始出现在人们的眼中。一经问世,它简约的设计风格,优美的线条就深深的吸引住了人们的眼球,佩戴这款腕表出席任何场合都显得游刃有余,一时间“简约”“包豪斯”成了腕表的代名词,风靡全球。

(Konkrete Komposition,1967)

(马克思·比尔—为德国荣汉斯钟表品牌设计了几款机械表)

(1-4 um excentrum IV,1969,风格:具体主义,类型:抽象)

(Gr&üner Kern,1971,风格:具体主义,类型:抽象)

(无题,1972,风格:具体主义,类型:抽象)

(无题,1978,风格:具体主义,类型:抽象)
比尔用数理模式为艺术注入了新的生命力。他将数理模式中的逻辑性、秩序性、无限性、复制性融入到他的作品中,使他的每个作品不再是孤立的、静止的,而是联系的、运动的艺术。他的变异作品也就不仅仅是15个,可以变化出150个、1500个,甚至更多。
数学有着严密的推理和逻辑的论证过程,而艺术是自身哲学理念和感性认识最直接的表现形式。这两门看似无关的学科在马克思·比尔作品中却得到了完美的结合。他运用几何图形、色彩的有序排列、搭配以及将形式语言进行了规律化、逻辑化的组合,形成了一系列有着强烈运动感的、相互关联的并可无限发展的艺术作品。读他的艺术作品,我们似乎能够感觉到作品不断发展、不断成长的内在生命力的存在。比尔用他的作品为我们阐述了一个全新的艺术表现形式–形的外衣、数的骨架。
马克思·比尔的作品始终围绕着数理模式,利用不同逻辑原理组合出不同的艺术效果,把逻辑的严谨性、有序性作为艺术的创作手段,把理性的数学规律应用于感性的艺术构想中,并以二者相结合的创作手法表达出来。这使我们在欣赏他的作品同时可以感受到逻辑的思维无处不在,正是这种数学逻辑的存在,透过艺术作品静止的形式外衣,我们感觉到了隐含在作品下面运动、发展、变化的数学规律。马克思·比尔的作品中大量地运用规律性的数学语言进行创作,并以全新的艺术表现形式将这一艺术创作思想推向了一个新的高度。
